Nonlinear conductance and heterogeneity of voltage-gated ion channels allow defining electrical surface domains in cell membranes

•Spatial domains of different electrical characteristics coexist on the cell surface.•A phenomenological model for voltage-gated channels over the cell membrane is used.•Channels of distinct characteristics induce different sensitivities over the membrane.•Domains of different properties locally modulate electrical signals over the membrane.

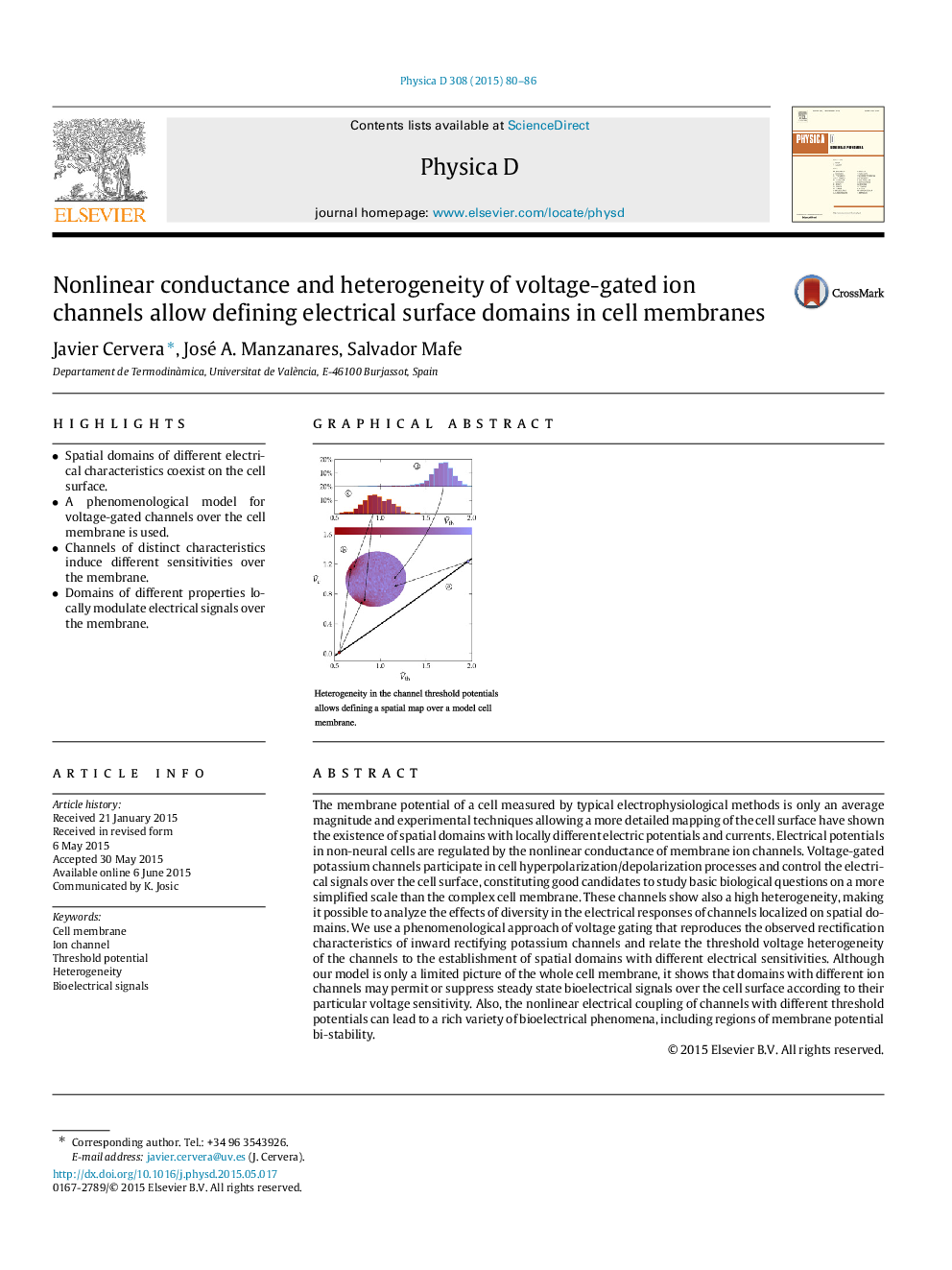
The membrane potential of a cell measured by typical electrophysiological methods is only an average magnitude and experimental techniques allowing a more detailed mapping of the cell surface have shown the existence of spatial domains with locally different electric potentials and currents. Electrical potentials in non-neural cells are regulated by the nonlinear conductance of membrane ion channels. Voltage-gated potassium channels participate in cell hyperpolarization/depolarization processes and control the electrical signals over the cell surface, constituting good candidates to study basic biological questions on a more simplified scale than the complex cell membrane. These channels show also a high heterogeneity, making it possible to analyze the effects of diversity in the electrical responses of channels localized on spatial domains. We use a phenomenological approach of voltage gating that reproduces the observed rectification characteristics of inward rectifying potassium channels and relate the threshold voltage heterogeneity of the channels to the establishment of spatial domains with different electrical sensitivities. Although our model is only a limited picture of the whole cell membrane, it shows that domains with different ion channels may permit or suppress steady state bioelectrical signals over the cell surface according to their particular voltage sensitivity. Also, the nonlinear electrical coupling of channels with different threshold potentials can lead to a rich variety of bioelectrical phenomena, including regions of membrane potential bi-stability.

Graphical abstractFigure optionsDownload full-size imageDownload as PowerPoint slide