Spiralling dynamics near heteroclinic networks

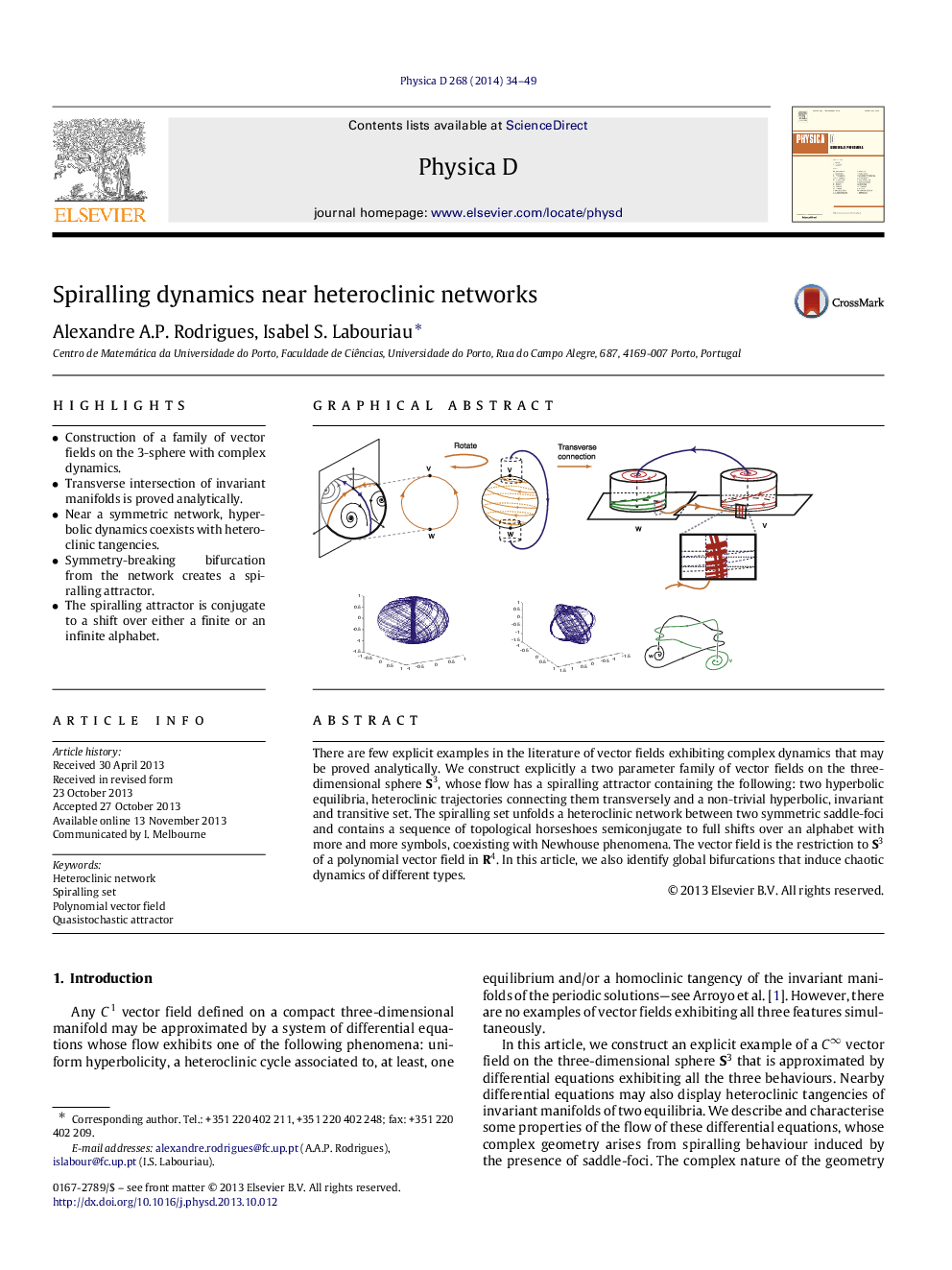
•Construction of a family of vector fields on the 3-sphere with complex dynamics.•Transverse intersection of invariant manifolds is proved analytically.•Near a symmetric network, hyperbolic dynamics coexists with heteroclinic tangencies.•Symmetry-breaking bifurcation from the network creates a spiralling attractor.•The spiralling attractor is conjugate to a shift over either a finite or an infinite alphabet.

There are few explicit examples in the literature of vector fields exhibiting complex dynamics that may be proved analytically. We construct explicitly a two parameter family of vector fields on the three-dimensional sphere S3, whose flow has a spiralling attractor containing the following: two hyperbolic equilibria, heteroclinic trajectories connecting them transversely and a non-trivial hyperbolic, invariant and transitive set. The spiralling set unfolds a heteroclinic network between two symmetric saddle-foci and contains a sequence of topological horseshoes semiconjugate to full shifts over an alphabet with more and more symbols, coexisting with Newhouse phenomena. The vector field is the restriction to S3 of a polynomial vector field in R4. In this article, we also identify global bifurcations that induce chaotic dynamics of different types.

Graphical abstractFigure optionsDownload full-size imageDownload as PowerPoint slide