| Article ID | Journal | Published Year | Pages | File Type |
|---|---|---|---|---|
| 709358 | IFAC Proceedings Volumes | 2013 | 6 Pages |
Abstract
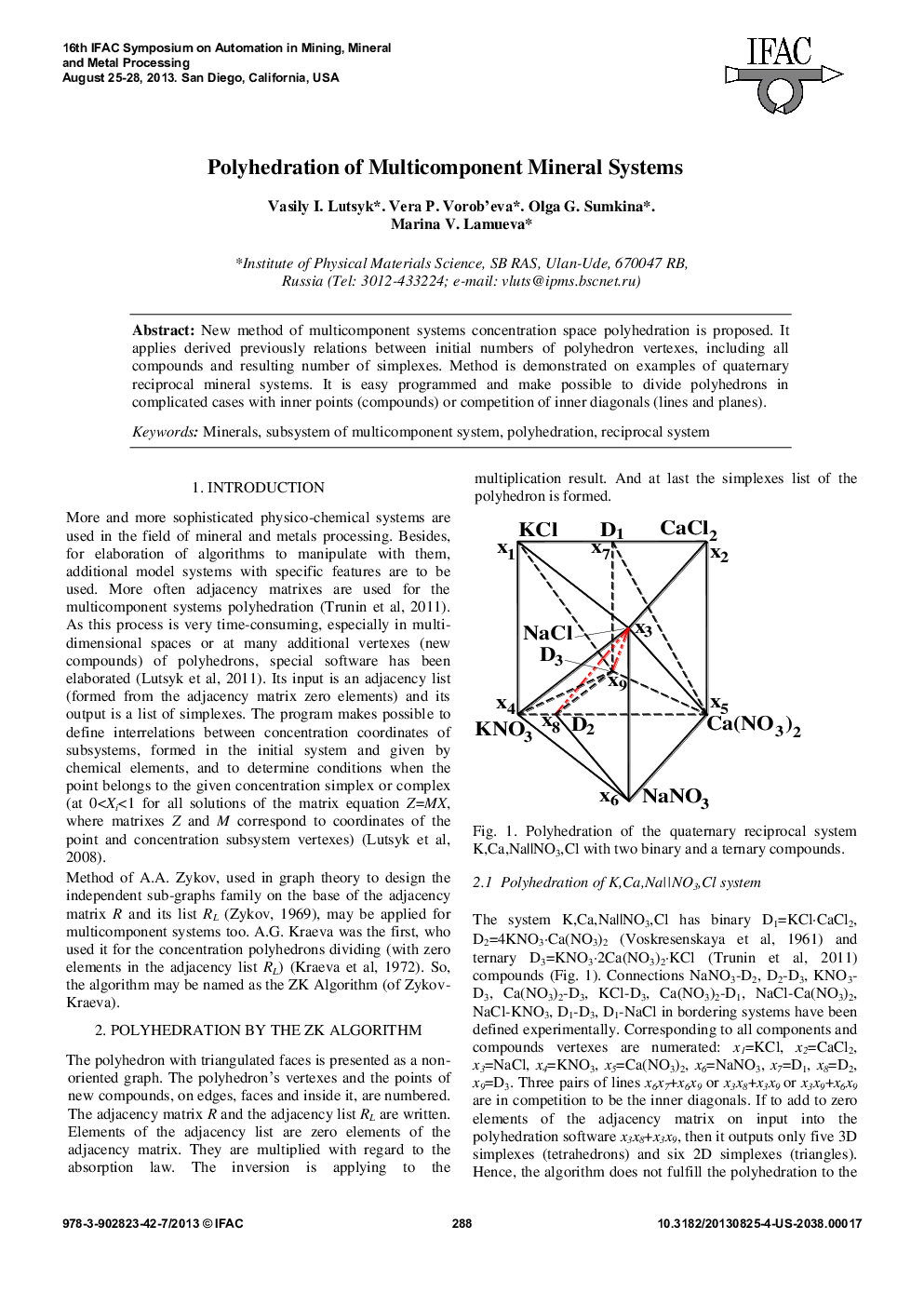
New method of multicomponent systems concentration space polyhedration is proposed. It applies derived previously relations between initial numbers of polyhedron vertexes, including all compounds and resulting number of simplexes. Method is demonstrated on examples of quaternary reciprocal mineral systems. It is easy programmed and make possible to divide polyhedrons in complicated cases with inner points (compounds) or competition of inner diagonals (lines and planes).
Related Topics
Physical Sciences and Engineering
Engineering
Computational Mechanics