Adjoint-based state and distributed parameter estimation in a switched hyperbolic overland flow model*

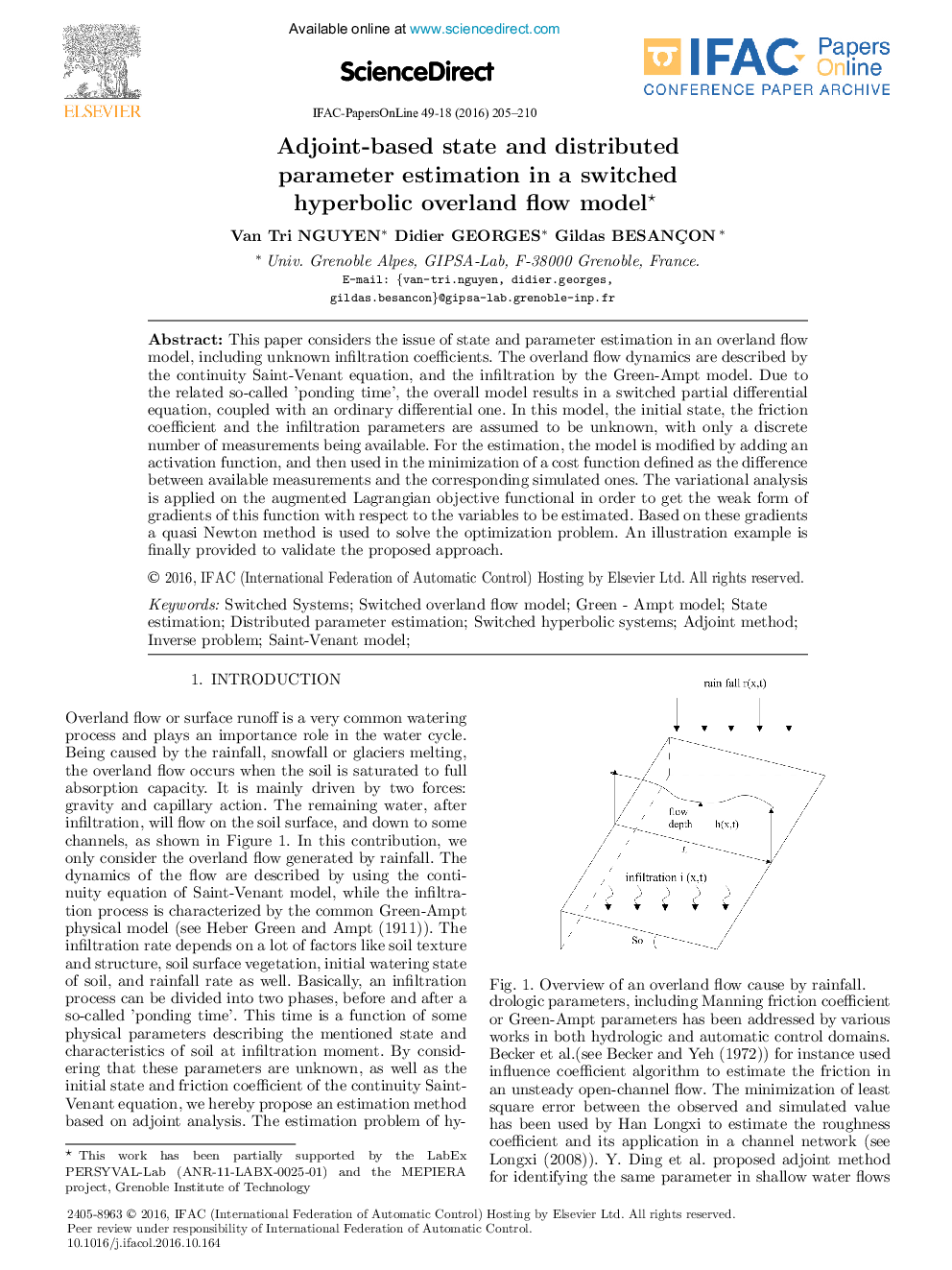
This paper considers the issue of state and parameter estimation in an overland flow model, including unknown infiltration coefficients. The overland flow dynamics are described by the continuity Saint-Venant equation, and the infiltration by the Green-Ampt model. Due to the related so-called 'ponding time', the overall model results in a switched partial differential equation, coupled with an ordinary differential one. In this model, the initial state, the friction coefficient and the infiltration parameters are assumed to be unknown, with only a discrete number of measurements being available. For the estimation, the model is modified by adding an activation function, and then used in the minimization of a cost function defined as the difference between available measurements and the corresponding simulated ones. The variational analysis is applied on the augmented Lagrangian objective functional in order to get the weak form of gradients of this function with respect to the variables to be estimated. Based on these gradients a quasi Newton method is used to solve the optimization problem. An illustration example is finally provided to validate the proposed approach.