The homological perturbation lemma and its applications to robust stabilization

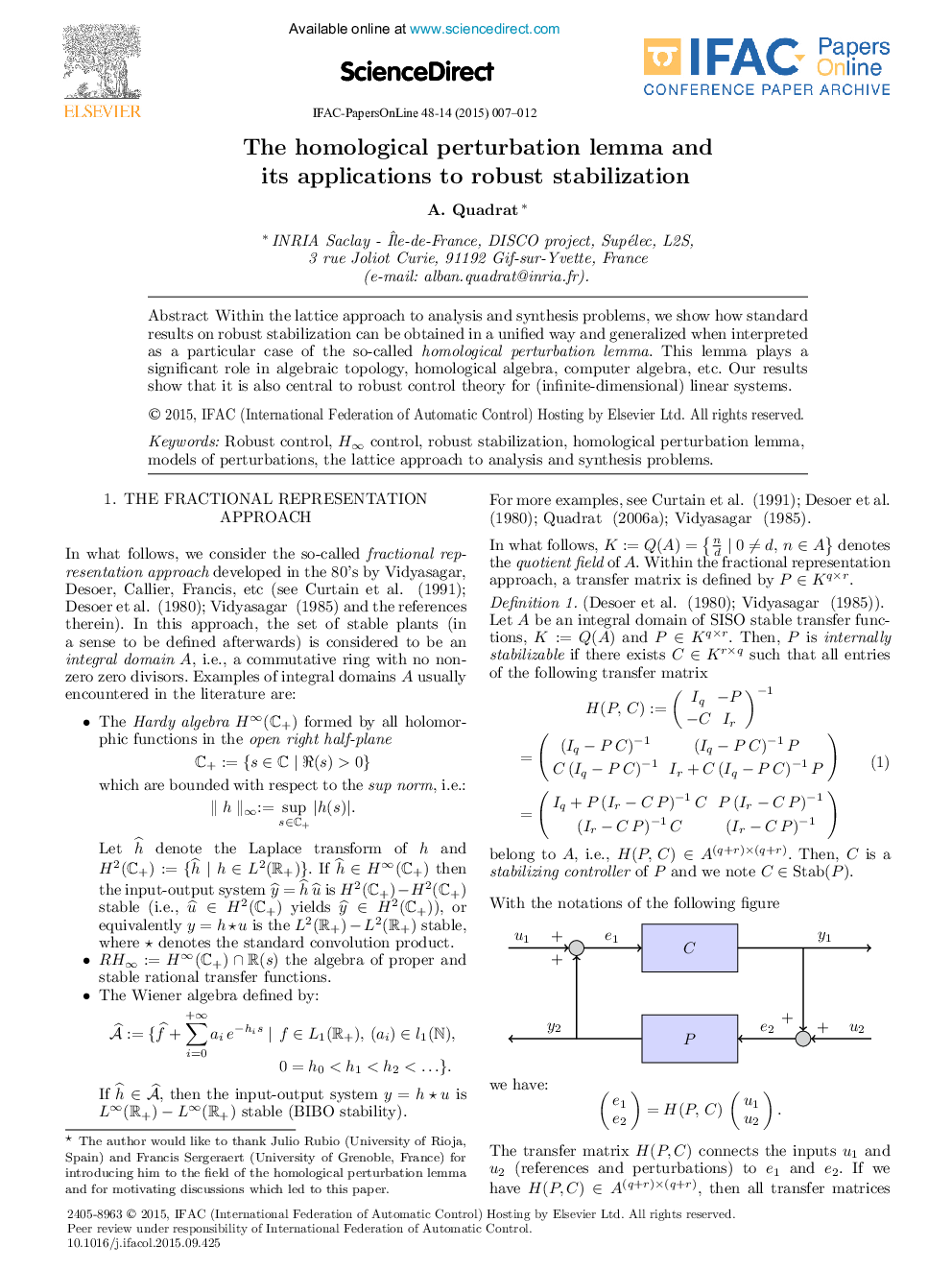
Within the lattice approach to analysis and synthesis problems, we show how standard results on robust stabilization can be obtained in a unified way and generalized when interpreted as a particular case of the so-called homological perturbation lemma. This lemma plays a significant role in algebraic topology, homological algebra, computer algebra, etc. Our results show that it is also central to robust control theory for (infinite-dimensional) linear systems.