The Attractors in the Complex Lorenz Model*

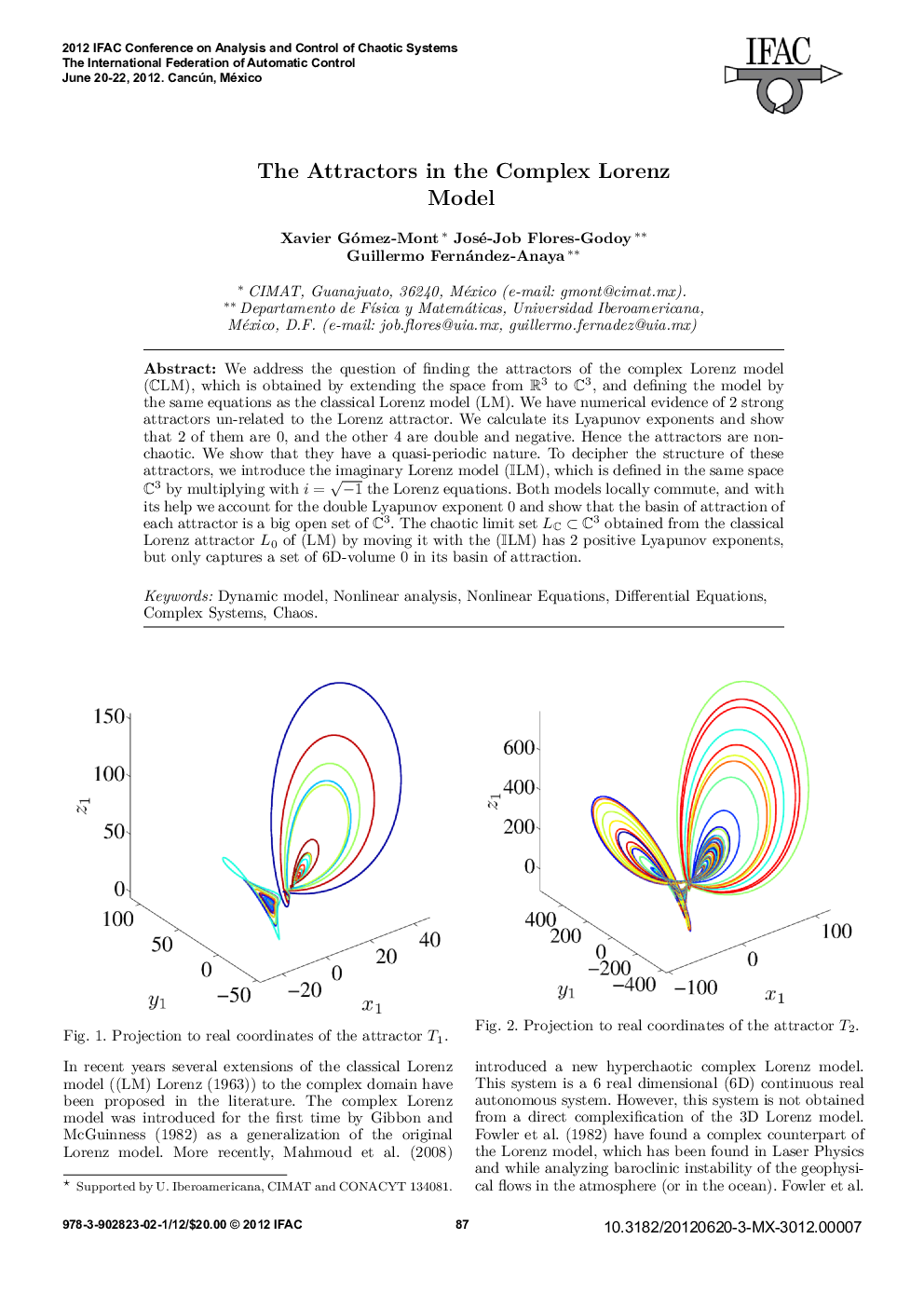
We address the question of finding the attractors of the complex Lorenz model (CLM), which is obtained by extending the space from ℝ3 to ℂ3, and defining the model by the same equations as the classical Lorenz model (LM). We have numerical evidence of 2 strong attractors un-related to the Lorenz attractor. We calculate its Lyapunov exponents and show that 2 of them are 0, and the other 4 are double and negative. Hence the attractors are non-chaotic. We show that they have a quasi-periodic nature. To decipher the structure of these attractors, we introduce the imaginary Lorenz model (ILM), which is defined in the same space ℂ3 by multiplying with √−1 the Lorenz equations. Both models locally commute, and with its help we account for the double Lyapunov exponent 0 and show that the basin of attraction of each attractor is a big open set of ℂ3. The chaotic limit set Lℂ ⊂ ℂ3 obtained from the classical Lorenz attractor L0 of (LM) by moving it with the (ILM) has 2 positive Lyapunov exponents, but only captures a set of 6D-volume 0 in its basin of attraction.