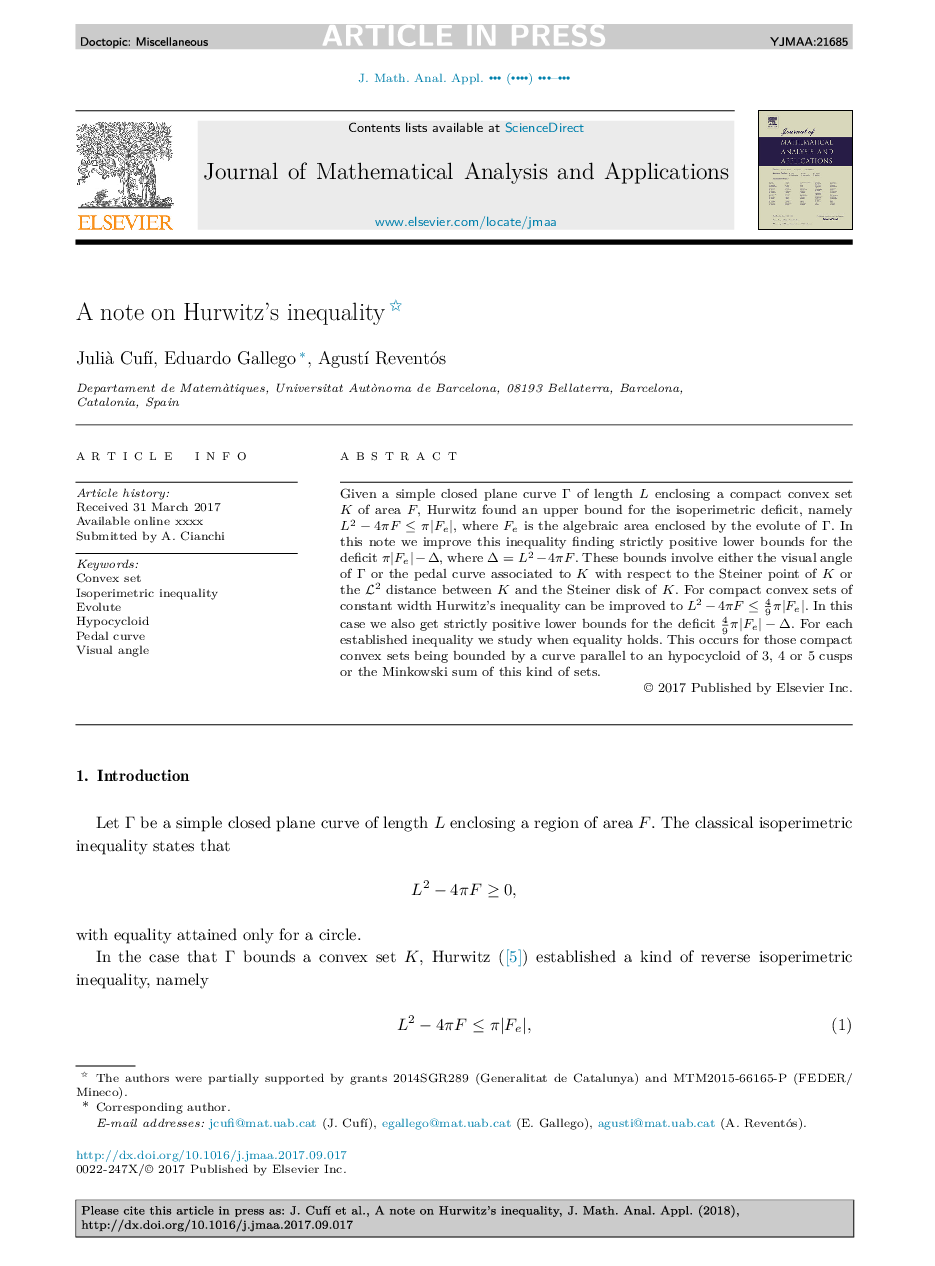
A note on Hurwitz's inequality

Given a simple closed plane curve Γ of length L enclosing a compact convex set K of area F, Hurwitz found an upper bound for the isoperimetric deficit, namely L2−4πF≤π|Fe|, where Fe is the algebraic area enclosed by the evolute of Γ. In this note we improve this inequality finding strictly positive lower bounds for the deficit π|Fe|−Δ, where Δ=L2−4πF. These bounds involve either the visual angle of Γ or the pedal curve associated to K with respect to the Steiner point of K or the L2 distance between K and the Steiner disk of K. For compact convex sets of constant width Hurwitz's inequality can be improved to L2−4πF≤49π|Fe|. In this case we also get strictly positive lower bounds for the deficit 49π|Fe|−Δ. For each established inequality we study when equality holds. This occurs for those compact convex sets being bounded by a curve parallel to an hypocycloid of 3, 4 or 5 cusps or the Minkowski sum of this kind of sets.